Phd Research
My research work was in the field of fluid mechanics, which is a vast topic that subdivides into many aspects e.g. turbulence, boundary layer theory, instability onset, hydrodynamics, arterial blood flow and secondary flow transitions. Under some circumstances (usually inviscid conditions, i.e. high Reynolds number) it is possible to make a comparison between aerodynamics and fluid mechanics. After all, water and air are simply mediums through which bodies move and this idea is preserved mathematically too. Below is a simulated animation of flow past a flat plate, as you can see, the dynamics are very intricate even for a flat obstacle!
University of London Thesis Reference British Library Thesis Reference
Download from Imperial College London
You can download adetailed summary of my thesis here; however, if you are feeling particularly brave and want the genuine article then you may download that here .
Problem 1: concentric cylinder flow
In my Phd, I investigated two problems. In the first problem, the possible onset of chaotic flow originating from a stable state was investigated. The fluid starts off at rest and is contained within two concentric vertically aligned cylinders. The viscous fluid is then driven by the periodic motion of transversely oscillating inner cylinder. There are good reasons to expect that the governing equations for this scenario will support chaotic solutions. However, if chaotic configurations do exist, which ones are the preferred states for the motion? i.e. if two or more solutions coexist at the same Reynolds number, which one is formed most readily? The study of this problem leads us into the realm of shock formation (thin layers in the fluid where rapid changes occur in the motion).
Problem 1: diagram of the setup

Problem 1: governing equations
The stream function for the above flow obeys the following PDE
$$\begin{equation}\label{p1introhpa}
\Psi _{\eta \eta \tau } = \frac{1}{{R_s }}\Psi _{\eta \eta \eta \eta } +
\Psi _{\eta \eta \eta } \Psi _\theta - \Psi _{\eta \eta \theta } \Psi _\eta
\end{equation}$$
subject to the boundary conditions
$$\begin{equation}
\Psi(\theta=0)=0, \quad\Psi(\eta=\pm 1)=0, \quad \Psi_{\eta}(\eta=\pm 1)= -\sin \theta .
\end{equation}$$
Problem 1: depiction of flow in stable state 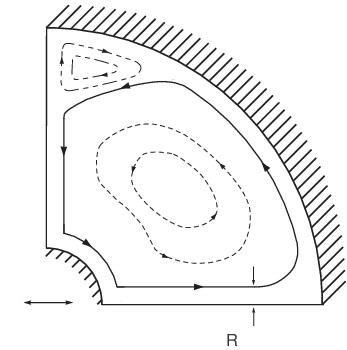
Problem 2: torsionally oscillating pipe flow

In the second problem, the onset of an instability in a circular pipe is investigated. The horizontal pipe containing the fluid is oscillated torsionally and it is predicted that thin tube like rolls will form on the inner surface of the pipe. The onset of the this new instability is predicted using a theory developed by Soward and Jones. The latter authors propose that in order to correctly predict the onset of instability for cylindrical/ spherical geometries, it is necessary to solve the governing eigenvalue equations in the complex plane (the algebraic/ numerical construction of the physical solution is a hellish nightmare!). Despite their appearance the basic flow equations are fairly easy to solve for small amplitude oscillations and PDEs governing the latter flow are:
$$\begin{equation}
\frac{1}{r}\psi _{\theta \theta t} + \psi _{rt} + r\psi _{rrt} = -
2\sin t(w^{\scriptscriptstyle (0)}_\theta \cos \theta +
rw_r^{\scriptscriptstyle (0)} \sin \theta ) + \frac{1}{\mathit{\Phi}}\big(
r\psi _{rrrr} + 2\psi _{rrr} \\ - \frac{1}{r}\psi _{rr}+ \frac{2}{r}\psi
_{\theta \theta rr} + \frac{1}{{r^2 }}\psi _r - \frac{2}{{r^2 }}\psi
_{\theta \theta r}+ \frac{1}{{r^3 }} \psi _{\theta \theta \theta \theta }
+ \frac{4}{{r^3 }}\psi _{\theta \theta }\big)
\end{equation}$$
where
$$\begin{equation}\label{p2basicw}
w^{\scriptscriptstyle (0)}=e^{it}\cos\theta \big[-ir+k_1\;J_1(r\lambda)
\big]+\mathrm{c.c} \ , \quad k_1=\frac{i}{2J_1(\lambda/2)} \quad \mathrm{and}\quad \psi_\theta = 0,\quad \psi_r = 0 \quad \mathrm{at} \quad r = \frac{1}{2}
\end{equation}$$
For high frequencies the flow is found to exhibit roll type instabilities, which manifest in a similar fashion to the turbulent rolls in the illustrations below.


